Numberphile and Neo4J numbers experimentations
| | 3 minutes | 428 words
Since the last post about Neo4J, I had to work on some project not involving it unfortunately.
However, being a regular user of Numberphile, I came across a specific video footage and I had the idea that we could find the solution to it using Neo4J.
In this video, Matt Parker discusses a puzzle problem involving square sums.
The video shows how to link a list of numbers from 1 to 15, such that adjacent numbers sums are perfect square numbers.
I had a vague idea but I wasn’t sure, that the solution to this problem could be found using Neo4J.
So I started up Neo4J Desktop and started to play with CYPHER queries.
I first created the list of nodes of type “Number”:
FOREACH (n IN range(1,20) | CREATE (:Number {value: n}))
This query will create twenty nodes of type “Number” having a specific property “value”. That property value will go from 1 to 20.
The list of all the node of type Number
Then, we need to find how to arrange those numbers so they match the puzzle explained in the Numberphile’s video.
In order to create the good relationships between those numbers, we have to transform the matching property “the sum of adjacent numbers is a perfect square number” into the Cypher Query Language.
MATCH (n1:Number), (n2:Number)
We match two nodes, they can be the same or not, for now we don’t care.
WHERE sqrt(n1.value + n2.value) % 1 = 0
Where the rest of the square root of the sum of the property value of those nodes is zero. Indeed, the rest of the division by 1 of the square root of a square number will always be an integer.
AND id(n1) > id(n2)
Where those nodes are different from each other.
MERGE (n2)-[:LinkedTo]-(n1)
Then create the relationship “LinkedTo” if it doesn’t exist yet.
RETURN *
And return all the objects.
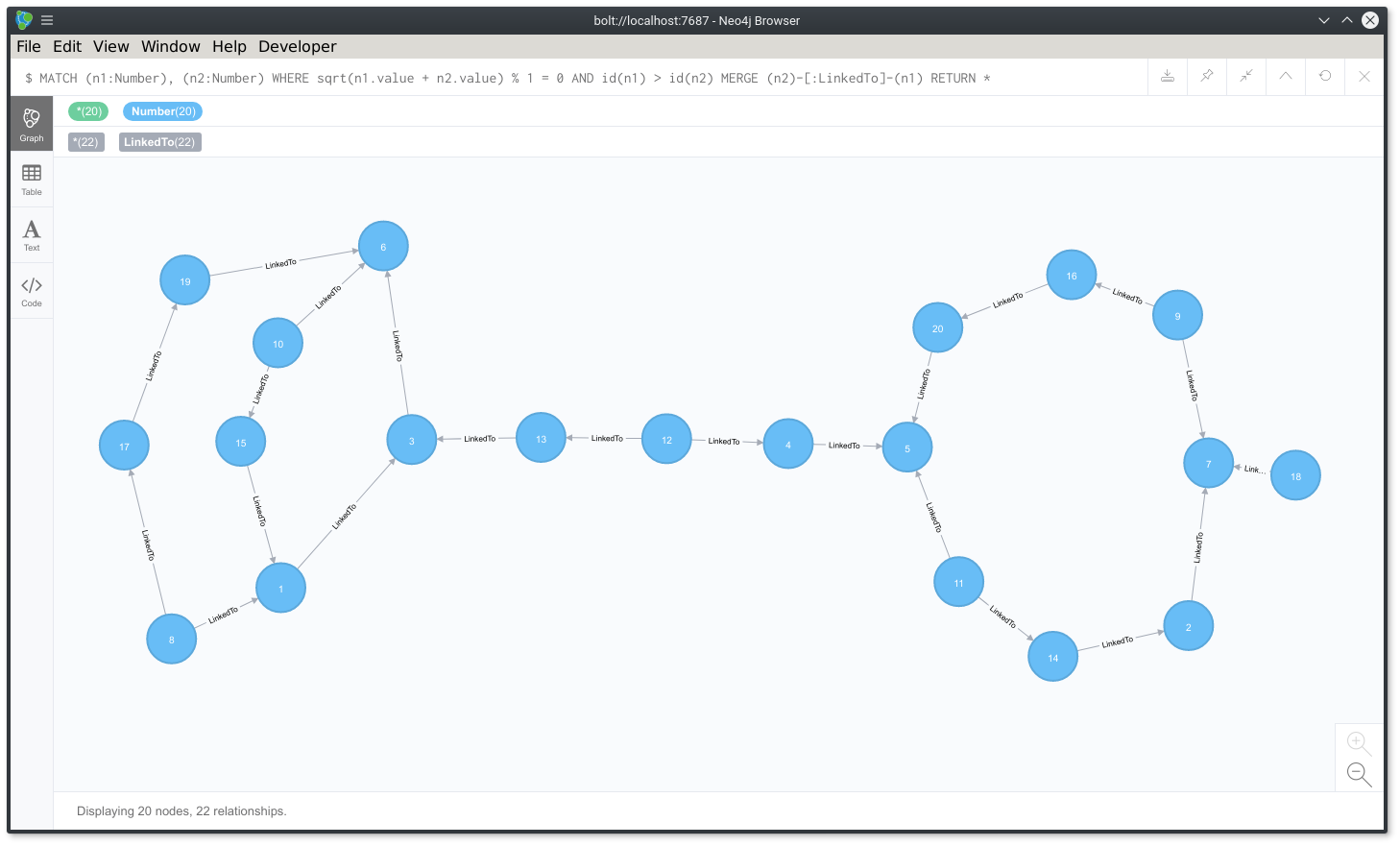
The list of all the node of type Number linked from 1 to 20
You can now clearly see if you sum up every every pair of adjacent nodes, it’s a perfect square number.
If you want to retry the experience with bigger figures, delete everything:
MATCH (n) DETACH DELETE n
And restart using numbers like… 50!
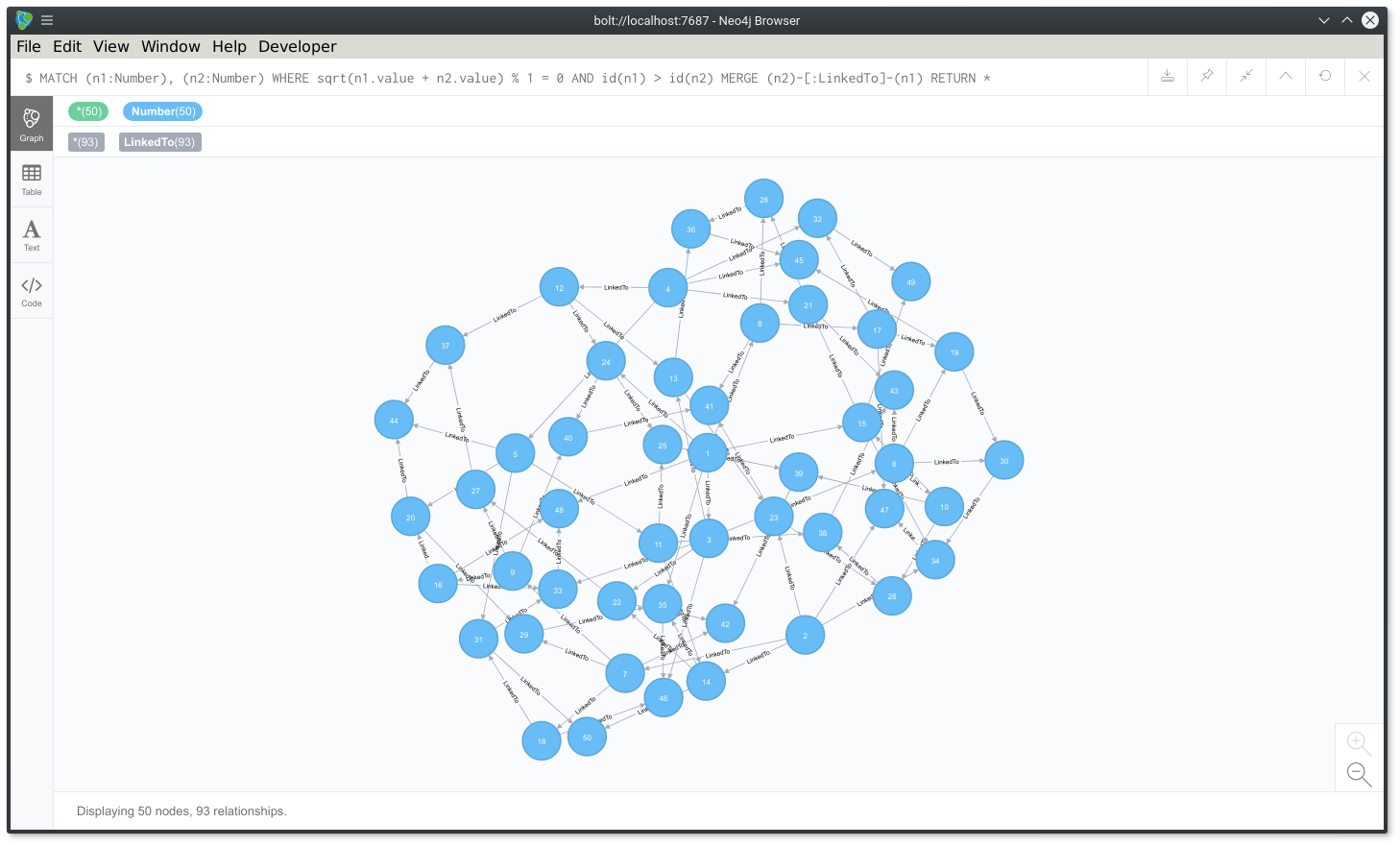
The list of all the node of type Number linked from 1 to 50
It works fine, however I guess you’ve seen the issue… Some nodes have more than two relationships.
Do you think you could find the right Cypher query to prevent this ?
If yes, don’t hesitate to post it in the comments !